2. 兩者都是增函數(shù)；兩者都是2k和2k+上的減函數(shù)（kz）。兩者都是（k-,k+）上的增函數(shù)（kz）。兩者都是（k,k+）上的減函數(shù)（kz）。反三角函數(shù)的圖形。反三角函數(shù)的性質(zhì)。名稱。反正弦函數(shù)。反余弦函數(shù)。反正切函數(shù)。反余切函數(shù)。定義。y=sinx(x-, )。反函數(shù)稱為反正弦函數(shù)，記為x==cosx(x0,)。 反函數(shù)叫做反余弦函數(shù)，記為x==tanx(x(-, )。反函數(shù)叫做反正切函數(shù)，記為x==cotx(x(0,)。反函數(shù)叫做反余切函數(shù)常用反函數(shù)公式大全，記為x=。理解。屬于-網(wǎng)校哪個(gè)好，且正弦值等于x的角度屬于0，余弦值等于x的角度屬于（

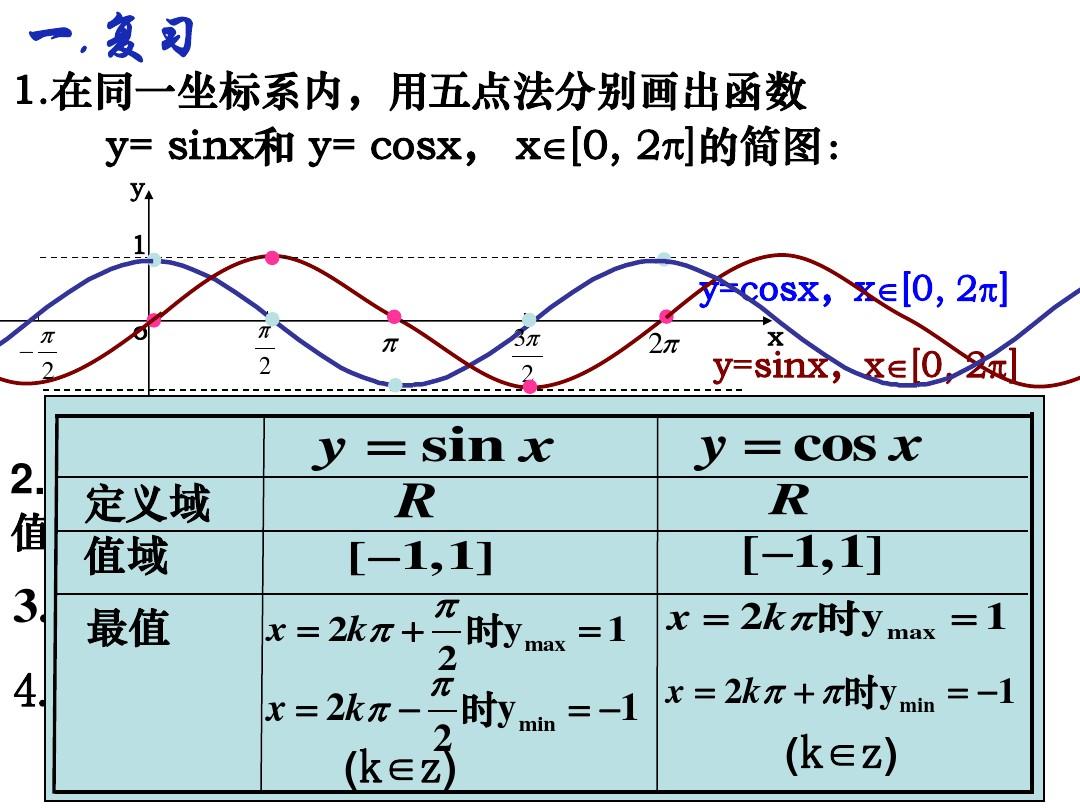
3. -,)，正切等于x的角表示屬于(0,)，余切等于x的角表示屬于(0,)。 性質(zhì)： 定義域：-1, 1-1, 1(-, +)(-, +) 值域：-, 0, (-,)(0,) 單調(diào)性：-1, 1上為增函數(shù)：-1, 1上為減函數(shù)：(-, +)上為增函數(shù)：(-, +)上為減函數(shù)：奇偶性：(-x) = -(-x) = -(-x) = - 周期性：都不是同步函數(shù)。 恒等式：sin() = x(x-1, 1)(sinx) = x(x-,)cos() = x(x-1, 1) (cosx) = x(x0,)tan(arcta

4. nx)=x(xr)(tanx)=x（x(-,)）cot()=x(xr)(cotx)=x(x(0,) 互補(bǔ)恒等式 +=(x-1,1)+=(xr) 三角函數(shù)公式 二角公式 sin(a+b) = + sin(ab) = - cos(a+b) = - cos(ab) = + tan(a+b) =tan(ab) =cot(a+b) =cot(ab) = 雙角公式 tan2a =sin2a=

5. = cos2a-sin2a=-1=1-三角公式 sin3a = 3sina-4(sina) = 4(cosa)3- = tana·tan(+a)·tan(-a)半角公式 sin()=cos()=tan()=cot()= tan()=乘積和 sina+sinb=-sinb=+cosb = -cosb = -+tanb=乘積和= -cos(a+b)-cos(ab) =

6. cos(a+b)+cos(ab) = sin(a+b)+sin(ab) = sin(a+b)-sin(ab) 誘導(dǎo)公式 sin(-a) = -(-a) = (-a) = (+a) = (+a) = -(-a) = (-a) = -(+a) = -(+a) = -=tana = 通用公式 sina=cosa=tana=其他公式 asina+bcosa=×sin(a+c) 其中 tanc=asin(a)-b

7. cos(a) = ×cos(ac) 其中 tan(c)=1+sin(a) =(sin+cos)21-sin(a) = (sin-cos)2其他非關(guān)鍵三角函數(shù) csc(a) = sec(a) = 雙曲函數(shù) sinh(a)=cosh(a)=tg h(a)=公式1：對(duì)于任意角，具有相同終邊的角的相同三角函數(shù)值相等： sin(2k)= sin cos(2k)= cos tan(2k)= tan cot(2k)= cot 公式2：對(duì)于任意角常用反函數(shù)公式大全，+的三角函數(shù)值與的三角函數(shù)值之間的關(guān)系為： sin()= -sin cos()= -cos tan()= tan cot()= cot 公式3：任意角的三角函數(shù)與-

8. 值之間的關(guān)系：sin(-) = -sin cos(-) = cos tan(-) = -tan cot(-) = -cot 公式4 利用公式2和公式3，我們可以得到 - 和 的三角函數(shù)值之間的關(guān)系：sin(-) = sin cos(-) = -cos tan(-) = -tan cot(-) = -cot 公式5 利用公式-和公式3，我們可以得到2- 和 的三角函數(shù)值之間的關(guān)系：sin(2-) = -sin cos(2-) = cos tan(2-) = -tan cot(2-) = -cot 公式6 ± 和 ± 的三角函數(shù)值之間的關(guān)系：sin(+) = cos cos(+) = -sin tan(+) = -cot co

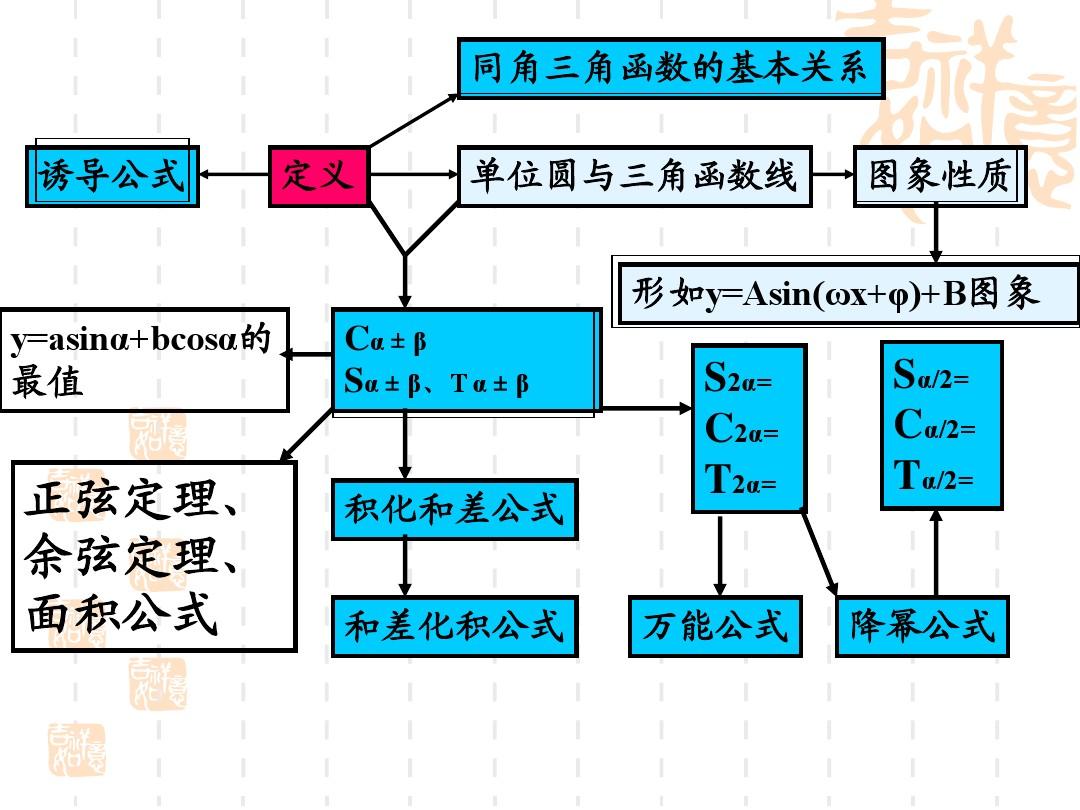
9. t(+) = -tan sin(-) = cos cos(-) = sin tan(-) = cot cot(-) = tan sin(+) = -cos cos(+) = sin tan(+) = -cot cot(+) = -tan sin(-) = -cos cos(-) = -sin tan(-) = cot cot(-) = tan （上面的kz） 我花了很長(zhǎng)時(shí)間才把這個(gè)常見(jiàn)的物理公式打出來(lái)，希望對(duì)大家有用。 a sin(t+) + bsin(t+) = × sin 三角公式證明（全部） 公式表達(dá)式 乘法和因式分解 a2-b2=(a+b)(ab) a3+b3=(a+b)(a2-ab+b2) a3-b3=(ab)

10. (a2+ab+b2) 三角不等式 |a+b|a|+|b| |ab|a|+|b| |a|b-bab |ab|a|-|b| -|a|a|a| 二次方程的解 -b+(b2-4ac)/2a -b-b+(b2-4ac)/2a 根與系數(shù)的關(guān)系 x1+x2=-b/a x1*x2=c/a 注意：韋達(dá)定理判別式 b2-4a=0 注意：該方程有兩個(gè)相等的實(shí)根 b2-4ac>0 注意：該方程有一個(gè)實(shí)根 b2-4ac

11. - cos(ab)=+ tan(a+b)=(tana+tanb)/(1-) tan(ab)=(tana-tanb)/(1+) ctg(a+b)=(-1)/(ctgb+ctga) ctg(ab)=(+1)/(ctgb-ctga) 雙角度公式 tan2a=2tana/(1-tan2a) ctg2a=(ctg2a-1)/2ctga cos2a=cos2a-sin2a=-1=1- 半角度公式 sin(a/2)=(1-cosa)/2) sin(a/2)

12. =-(1-cosa)/2) cos(a/2)=(1+cosa)/2) cos(a/2)=-(1+cosa)/2) tan(a/2)=(1-cosa)/(1+cosa) tan(a/2)=-(1-cosa)/(1+cosa) ctg(a/2)=(1+cosa)/(1-cosa) ctg(a/2)=-(1+cosa)/(1-cosa) 和差積=sin(a+b)+sin(ab) =sin(a+b)-sin(ab) =cos(a+b)-sin(ab) -=cos(a+b)-cos(ab) sina+sinb=2sin(

13. a+b)/2)cos(ab)/2 cosa+cosb=2cos(a+b)/2)sin(ab)/2) tana+tanb=sin(a+b)/ tana-tanb=sin(ab)/ ctga+(a+b)/ -ctga+(a+b)/ 某些序列前 n 項(xiàng)之和 1+2+3+4+5+6+7+8+9+n=n(n+1)/2 1+3??+5+7+9+11+13+15+(2n-1)=n2 2+4+6+8+10+12+14+(2n)=n(n+1) 12+22+32+42+52+62+72+82+n2=n(n+1)(2n+1)/6

14、 13+23+33+43+53+63+n3=n2(n+1)2/4 1*2+2*3+3*4+4*5+5*6+6*7+n(n+1)=n(n+1)(n+2)/3 正弦定理 a/sina=b/sinb=c/sinc=2r 注：r 為三角形外接圓半徑 余弦定理 b2=a2+c2- 注：角 b 為邊 a 與邊 c 的夾角 正切定理 (a+b)/(ab)=tan(a+b)/2/tan(ab)/2 圓的標(biāo)準(zhǔn)方程 (xa)2+(yb)2=r2 注：(a,b) 為圓心坐標(biāo) 圓的一般方程 x2+y2+dx+ey+f=0 注：d2+e2-4f>0拋物線的標(biāo)準(zhǔn)方程 y2=2px y2=-2px x2

15. =2py x2=-2py 直棱柱的側(cè)面積為s=c*h 斜棱柱的側(cè)面積為s=c'*h 直金字塔的側(cè)面積為s=1/2c*h' 直圓錐的側(cè)面積為s=1/2(c+c')h' 平截頭體的側(cè)面積為s=1/2(c+c')l=pi(r+r)l 球的表面積為s=4pi*r2 圓柱的側(cè)面積為s=c*h=2pi*h 圓錐的側(cè)面積為s=1/2*c*l=pi*r*l 弧長(zhǎng)公式l=a*ra為圓心角r>0的弧度 扇形的面積公式為s=1/2*l*r 圓錐的體積公式為 v=1/3*s*h 圓錐的體積公式為v=1/3*pi*r2h 斜棱柱的體積為v=s'l 注：其中s'為直截面面積，l為邊棱柱的長(zhǎng)度 棱柱的體積公式為v=s*h圓柱體v=pi*r2h 【本課件下載后可自行編輯修改，僅供參考，謝謝支持！ 】 23 / 23 實(shí)用的高質(zhì)量文檔