免費試聽
雙曲線 x^2/a^2-y^2/b^2 = 1 的簡單幾何性質：
1. 范圍：|x|≥a,y∈R。
2、對稱性：雙曲線的對稱性與橢圓的對稱性完全相同雙曲線漸近線公式，都是關于x軸、y軸和原點對稱。
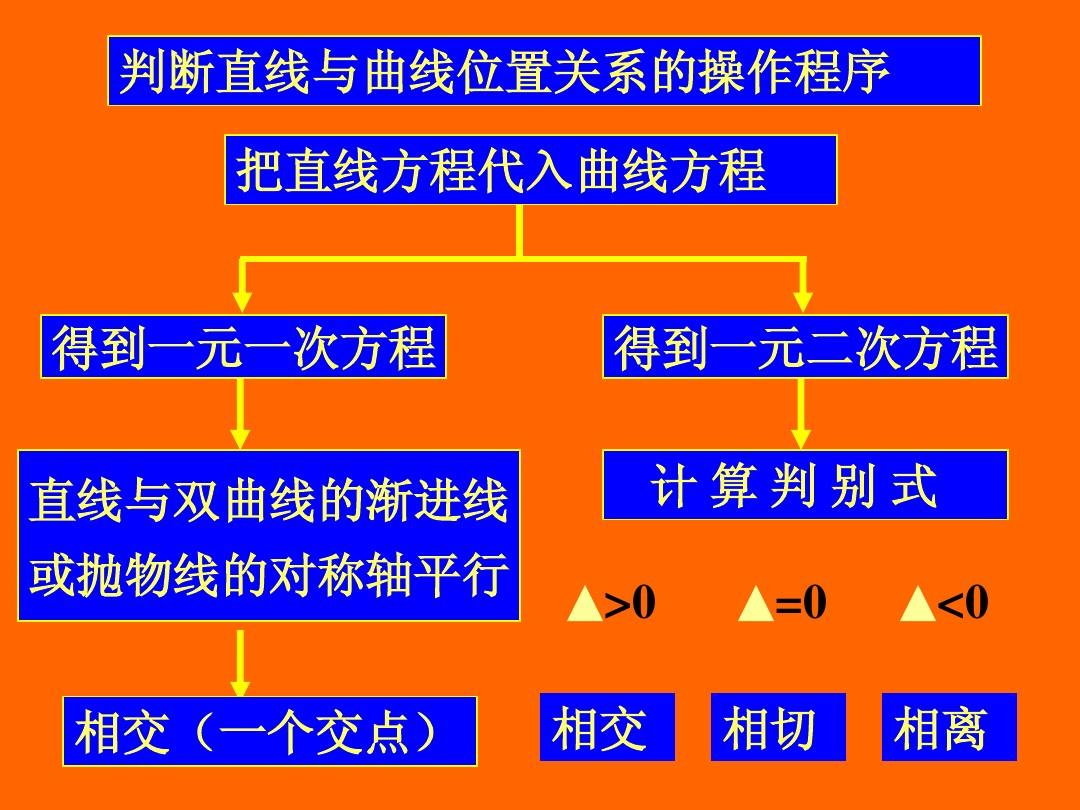
3. 頂點：有兩個頂點A1(-a,0)和A2(a,0)，兩頂點之間的線段為實軸雙曲線漸近線公式網校哪個好，長度為2a，虛軸為2b。而且c^2=a^2+b^2，這與橢圓不同。
漸近線特征：
無限接近，但不相交。分為垂直漸近線、水平漸近線和斜漸近線。當曲線上一點M沿曲線無限遠離原點時，若M到某直線的距離無限趨近于零，則此直線稱為該曲線的漸近線。
需要注意的是，并不是所有的曲線都有漸近線。漸近線反映的是某些曲線在無限延伸時的變化。根據漸近線的位置，漸近線可以分為三類：水平漸近線、垂直漸近線和斜漸近線。
y=k/x（k≠0）是反比例函數，其圖像關于原點對稱，x=0，y=0是它的漸近線方程。
當焦點在x軸上時，雙曲線漸近線的方程為y=[+(-)b/a]x。
焦點在y軸上時雙曲線漸近線的方程為y=[+(-)a/b]x。
名師輔導
環球網校
建工網校
會計網校
新東方
醫學教育
中小學學歷
今日
您現在的位置：
